Задание №1 (Интерполяция)
Задание 1: Самостоятельно напишите полином L4(x), проходящий через четыре узла.
Таким образом, чтобы выполнить задание диктанта и записать полином, в формулу нужно подставить координаты точек (никакого промежуточного расчета не делать, подобные не приводить!):
Доказательство прохождения полинома через точку
Если полином L(x) (как и всякая другая функция) проходит через точку (xi,yi), то, при подстановке в него х=xi, он должен иметь значение yi (т.е. L(xi)= yi).
Например:
Обратите внимание, ничего рассчитывать не требуется: в числителе 1го и 3его слагаемых есть скобка (3-3), которая превращает слагаемое в ноль. А во втором слагаемом скобки в числителе и знаменателе одинаковые и дробь превращается в 1.
Так будет и для других полиномов:
Задание 2: Решите задание
Постановка задачи интерполяции. Для узлов (-1,2),(2,3),(3,6),(4,7) записать формулу интерполяционного полинома Лагранжа, проходящего через 4 точки. Чему равно значение полинома при х=4? Доказать, что полином проходит через узел (-1,2)
Первые 2 человека, приславших правильно решенные задания, получат дополнительный балл к экзамену.
Постановка
задачи интерполяции. Для узлов
(-1,2),(2,3),(3,6),(4,7),(5,6) (могут быть другие наборы из
3-6 точек) записать формулу интерполяционного
полинома Лагранжа, проходящего через
5 (в других заданиях - через 2-6) точек. Чему равно значение
полинома при х=4? Доказать, что полином
проходит через узел (-1,2) (или другой).
Общие рекомендации.
Постановка задачи:
Дано: (xi,yi)-узлы интерполяции, i=0…n; и точка интерполяции хинт, которая принадлежит отрезку [x0,xn].
Найти: Значение функции y(x) в точке интерполяции хинт.
Формула интерполяционного полинома Лагранжа, проведенного через m узлов интерполяции, представляет собой сумму из m слагаемых. Каждое слагаемое содержит координату уi очередного узла, умноженный на дробь. Дробь в числителе содержит (m-1) скобок типа (x-xj), где j меняется, но не равна i. В знаменателе подобные скобки (xi-xj).
Примеры интерполяционных полиномов
Таким образом, чтобы выполнить задание диктанта и записать полином, в формулу нужно подставить координаты точек (никакого промежуточного расчета не делать, подобные не приводить!):
Если полином L(x) (как и всякая другая функция) проходит через точку (xi,yi), то, при подстановке в него х=xi, он должен иметь значение yi (т.е. L(xi)= yi).
Например:
Так будет и для других полиномов:
Задание 2: Решите задание
Постановка задачи интерполяции. Для узлов (-1,2),(2,3),(3,6),(4,7) записать формулу интерполяционного полинома Лагранжа, проходящего через 4 точки. Чему равно значение полинома при х=4? Доказать, что полином проходит через узел (-1,2)
Первые 2 человека, приславших правильно решенные задания, получат дополнительный балл к экзамену.
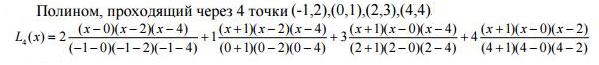
Комментариев нет:
Отправить комментарий